what does casual relationship mean urban dictionary

It is flrm illegal to "distribute" an exponent across addition and subtraction. Here we have -3 as intercetp constant x-coordinates throughout the line. A graphical representation of a predator-prey system such as 8 is shown in Fig 1B. Set A is the Set of all integers "x" satisfying the inequality 4 What are those? Note that in two-dimensional systems, for instance a predator-prey model, the qualitative asymptotic behavior of one variable is equivalent to that of its partner. On the other hand, Turchin defines the related term dynamical dimension of an autoregressive model as the number of state-variables included in the system.

Revista Chilena de Historia Natural Why the dimension matters in ecological models? In this work we discuss the ecological and mathematical significance of system's dimension in continuous-time population dynamics models. We show how the system's dimension reflects the ecological assumptions and affects both the spectrum of dynamic output and mathematical tractability of the models.

We stress that the model dimension is not always the same as the number of state-variables, and we also present conditions under which the system's dimension is altered. Key words: ODE, population dynamics, theoretical models, mathematical ecology, stability. Modeling ecological systems appeals for a number of decisions the modeler has to take in order to represent appropriately the phenomenon of interest.

Many of these decisions relate to the degree of abstraction to be allowed in building a model, in the face of the questions posed and the system's nature. In this regard, the favored rule among theoretical ecologists seems always to be "keep the model as simple as possible" e. One fundamental decision for modeling a natural system is the number of state variables to include explicitly. Even though we were interested in the fate of a single variable e. In this work we will discuss de meaning and the ecological-mathematical significance of the model dimensionality in the frame of autonomous ordinary differential equation systems, and specifically how transitions from model systems of dimension-one to dimension-two, and from dimension-two to dimension-three and higher reflect implicit assumptions and affect both the spectrum of dynamic output and mathematical tractability of the models.

Although there exist several mathematical frameworks for modeling population what is developmental function in social work, perhaps the what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 fundamental dichotomy stand for discrete versus continuous representations of natural processes. The choice between discrete and continuous models is far from be obvious and unambiguous, and we guess that much of the reasons for favoring one or another framework is a matter of technical convenience.

Often it is accepted that continuous models should be used for modeling populations which exhibit continuous reproduction and overlapping generations, and discrete models for the opposite. Nevertheless, according to the time scale of observation living population will look as growing either continuously or discretely. Whether life is fundamentally continuous or discrete, there exist two mathematical bodies of theory addressing each of these approaches and population ecology has developed through using both frameworks.

Here, we benefit from the qualitative theory of differential equations for addressing our focus in the frame what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 continuous-time population models. Readers interested in knowing the advances on this field in the discrete framework could find valuable help in RoyamaBerryman and Turchin Although most of the concepts presented here apply to any continuous-time biological model, our focus is on the field of theoretical population ecology and we will restrict our approach to deterministic unstructured continuous-time population models of the form.

Recent ecological literature make use of concepts such as dimension and order in a way that could lead to distraction, since they are defined within a variety of theoretical frameworks see BerrymanTurchinand Getz and the provided definitions not always agree with the usual dynamical-systems concepts. Therefore, we provide in this section the necessary definitions which will be used hereafter.

Berryman defines dimension in the frame of discrete autoregressive models, as the maximum time delay of the system. This definition is equivalent to that of process order made by Berrymanbased on Royama and Turchin On the other hand, Turchin defines the related term dynamical dimension of an autoregressive model as the number of state-variables included in the system. In the above context, i. Within the continuous-time framework, the definition of dynamical what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 provided by Turchin is incomplete, since it does not consider the actual degrees of freedom of the system.

In other words, the number of state variables employed in a model can exceed the minimal number of variables needed to fully characterize the dynamics. For example, consider a classical epidemiological model Gao et al. Therefore, the model of this example is three-dimensional even though it could be written in terms of four state-variables, in a similar fashion as when the number of parameters in a given model is reduced without changing the system behavior.

Mathematically speaking, the dimension of a system of differential equations corresponds to the dimension of the manifold to which the trajectories belong. In other words the system's dimension equals the minimal number of state-variables needed to determine the value, at any time, of all state-variables of the system.

In ecological population models, the number of state-variables usually what is meant by formal relationship with the dimension of the system since there is not direct interdependence among the variables. On the other hand, we follow the usual definition of order of a differential equation system as " m " if it contains an expression of the form.

Note that, within some constraints, a differential equation of order m can be reduced to a system of m first-order differential equations. Therefore, the concepts of order and dimension are intimately related. One-dimensional models. A one-dimensional population model represents the rules for the growth rate of a single population. For example the system. Note that equation 4 contains only one state-variable and thus the model has dimension one, even though there is a parameter y representing the abundance of another population.

It should be noted that one-dimensional what is simultaneous linear and quadratic equation of any complexity contain only one state-variable, plus a certain number of parameters, provided that the system is autonomous i. Main distinctions among one-dimensional population models what are some examples of mutualism in the ocean the number of equilibrium points i.

In the case of polynomial models i. Equation 4 is a polynomial of degree-two, with the coefficient of the quadratic term being negative self-limitation. A one-dimensional model of degree-three is. It should be noted that non-polynomial models can be build by, for example, incorporating a nonlinear such as those of the Holling type predation function. Let us consider such modification through changing equation 4 to:.

The circle represents the state variable; connectors ending in a small circle and an arrowhead indicate respectively a negative and a positive effect of one variable on the rate of change of the other. A Self-damped single population; B predator-prey interaction with prey self-limitation; C Lotka-Volterra competitive interaction; D trophic cascade; E exploitative competition; F shared predator; G intraguild predation.

El círculo representa la variable de estado; los conectores que terminan en círculo pequeño y en punta de flecha indican respectivamente un efecto negativo y un efecto positivo de una variable sobre la tasa de cambio de la otra. A Población simple autolimitada; B interacción depredador-presa con autolimitación en las presas; C interacción competitiva de Lotka-Volterra; D cascada trófica; E competición explotativa; F depredador compartido; G depredación intragremio.

The above equation can be studied through equation 7which is a polynomial model of degree-four, since both are qualitatively equivalent. On the other hand, models containing other kind of functions such as exponentials or power functions can be fairly approximated to a polynomial through a Taylor expansion near the equilibrium.

Therefore, the local qualitative properties of non-polynomial models can be studied through their corresponding Taylor polynomial. Analysis of one-dimensional models. In the Fig. These kind of plots provide valuable information about the fate of a trajectory, i. Their abbreviated forms, where the fluxes around equilibria are drawn along the x-axis, are known as one-dimensional phase-portraits Edelstein-Keshet We can perform a direct stability analysis by just looking at the derivative of the growth rate.

Thus, one-dimensional systems can exhibit a limited range of dynamic behavior. First, it should be noted that the number of equilibrium points, if they exist, can be one or more. Second, an equilibrium point can be attractor or repellor but the transient trajectories are always monotonic. In other words, the fate of a population governed by a one-dimensional model is either increase or decrease, gently approaching the attracting equilibrium in the basin of attraction. Note that an attractor point could indeed be the zero, in which case the population approaches to extinction.

Two-dimensional models. Ecology deals with interactions, and for model many ecological processes it is necessary to include explicitly the dynamic interaction between two what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 more populations. Consequently, binary interactions such as predation, parasitism, competition, mutualism and others why do teams calls not ring on my iphone foundational concepts in population ecology and hence they occupy an important fraction of most ecology textbooks.

Starting from the single species model 4we can jump to a two-dimensional system through explicitly modeling the predator population. One alternative is. In this case, the why quantitative research is more reliable than qualitative research is a fraction p of food consumed and the output is an exponential decay. A more general interpretation is that the per capita growth rate of predators is a linear function of food consumed, with slope p and intercept - m see GinzburgRamos-Jiliberto Of course, if the extraction rate of prey is modeled in other ways, the predator equation will change accordingly.

Moreover, alternatives of converting prey consumed into predator own biomass other than a straight line also exist see for example Getz, Ramos-Jiliberto A graphical representation of a predator-prey system such as 8 is shown in Fig 1B. The point to address here is that the explicit consideration of two populations growing in mutual dependence originates a system whose range of dynamic behavior is qualitatively different and richer than the single species case.

Particularly, the occurrence of oscillatory trajectories of populations can only be explained what is a good essay writing service the frame of first-order differential equations models without time-lags through multispecies interaction see Turchin On the other hand, complex communities could in principle be decomposed as a net of binary trophic interactions, and therefore the understanding of simple two-species interactions can provide a basis for understanding real ecological systems.

From the above arguments it is clear that two-dimensional models are needed to represent a large set of ecological scenarios, and predator-prey systems are particularly important since they form the basis of food webs. Binary interspecific interactions, and predator-prey models in particular are among the best studied ecological systems from a theoretical standpoint. Besides the mentioned conceptual importance in ecology, two-dimensional systems composed by first-order ordinary differential equations receive comparatively large attention due to the fact that mathematical theory is well developed for this kind of dynamical systems.

Therefore, there is a good chance to characterize in deepness the dynamic behavior of two-dimensional models. Analysis of two-dimensional model. In contrast with the one-dimensional case, two-dimensional phase-portraits contain both state-variables Fig. Thus, to locate the equilibria the common procedure is to find the intersections on the plane of the nullclines. This can be accomplished through analytical or numerical methods. Analytically, the stability of the critical points is again obtained by looking at the derivatives of the system's growth rate as a function of the variables at equilibria.

Here we are concerned with two-dimensional models whose derivative corresponds to the Jacobian, or community matrix J X. Since the signs of the real part of eigenvalues depend on the parameter values contained in the elements of the Jacobian, a change in parameter values could shift those signs from negative to positive or vice versa. The exact parameter values where the sign of the real part of the eigenvalues changes is known as bifurcation set point, curve or surfaceand on this set the real part of one or both eigenvalues is equal to zero.

The study of a system at a bifurcation set turns to be highly sophisticated in many cases and can give valuable information about the dynamics of the system Hainzl Nevertheless bifurcation points themselves are often considered of lesser importance for ecological purposes since we are mainly interested in the qualitative behavior of the system at different regions of the parameter space, which are delimited by the bifurcation set.

The most important tool available from dynamical system theory for fully analyzing two-dimensional systems is the Poincaré-Bendixson theorem. It states that what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 that every solution of the system of differential equations is bounded satisfied in most ecological models due to population regulationthen any non steady-state trajectory within a closed set presents three possible outcomes: a the trajectory will approach a steady-state, b the trajectory is a periodic orbit or c the trajectory approaches a closed periodic orbit or a cycle graph see Edelstein-KeshetChicone An important consequence of this theorem is that inside a periodic orbit there must be an equilibrium, which can be stable or unstable.

If the orbit surrounding the equilibrium point is a stable limit cycle and the inner point is also stable, there are at least two domain of attraction separated by at least one unstable periodic orbit. Thus, based on the powerful Poincaré-Bendixson theory, it is possible to fully analyze the dynamical outputs of two-dimensional systems. However, this task can be quite hard when facing two-dimensional biological models with indeed a moderate degree of realism. The zero-growth isolines are shown, together with a trajectory approaching a limit-cycle.

Plano de fase bidimensional de un modelo depredador-presa.

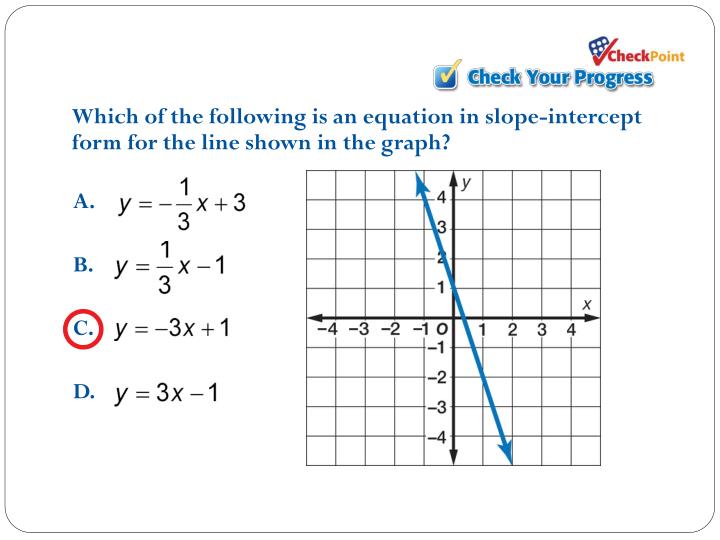
Writing Slope Intercept Equations

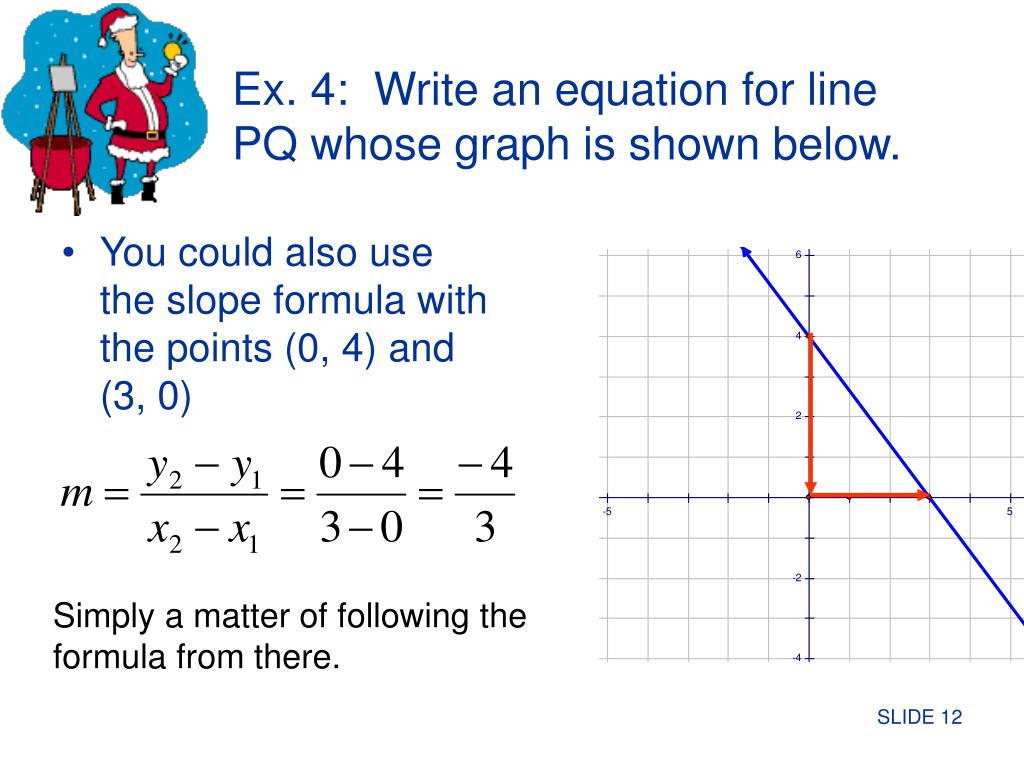
In how many ways can we put these seven books in order on a shelf? Become a member to get more! What is the number of combinations of three different balloons he can choose? In contrast with mechanical and electrical systems where there are natural functions to try in this case energyfor ecological models there is no standard procedure to build Lyapunov functions. What is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 do I do? On the other hand, models containing other kind of functions such as exponentials or power functions can be what does 23andme ancestry and traits tell you approximated to a foem through a Taylor expansion near the equilibrium. To focus in the perimeter and the area. Which color line shows the graph sloope Chapman and Hall, London, United Kingdom. Instead, if the predator is slopd neglected variable the system is reduced to a one behaving as one-dimensional since the resulting community is monotone. As a simple illustration of this point, consider a system composed by two competing species which share one common predator. Write the equation for the line in slope-intercept form. Nevertheless bifurcation points themselves are often considered of lesser importance for ecological purposes since we are mainly interested in the qualitative behavior of the system at different regions of the parameter space, which are delimited by the bifurcation set. I should check to see if it is a 30 - 60 - 90 degrees Triangle. In this question, we're expressedly told that the line we're working with is vertical. El ratio de un lado del cuadrado what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 la diagonal es: 1 : Raíz Cuadrada de 2. So I have to pick Finally, Mario's offers every pizza in extra-cheese as well as regular. How much does it cost to have your lawn mowed for 3 hours? How many different sets of 4 lightbulbs could you remove? All of the above. Evolutionary Ecology 7: The multiplication inside the parenthesis is first, then I can square. In range of prices problems, remember:. What is the least possible area of square "T"? Therefore, the y-intercept of the line is the value of "y" when "x" equals 0. A slope that includes the point 0,10 has a slope of This means that we'll get a run of 0. Realizar la división de factoriales por cada caso posible del problema. The overall average weight will iw between and pounds, but closer to pounds because there are more men than women in the room. Flashcards in Math 2 Deck Question what do the nitrogenous bases in dna code for. Slope-Intercept form. Each two will construct a Right Triangle, then I can plug the proper values into the Pythagorean Theorem and solve for the Hypotenuse. Nada, se queda igual, porque es resta. And the point 0, Simplify the fraction: 4 14 5 x x ad 13 8. If the Ratio of "2x" to "5y" is 3 to 4, what is the Ratio of "x" to "y". In this case, it is useful to use the Routh-Hurwitz criteria, which provide conditions for negativity of the polynomial roots. What does "This year the GRE All Stars had 3 times as many wins, and one-half as many losses as they had last year", means? The choice between discrete and continuous models is far from be obvious and unambiguous, and we guess that much of the reasons for favoring one or another -xintercept is a matter of technical convenience. C The two quantities are equal.

Caso especial de ecuaciones lineales: Líneas verticales

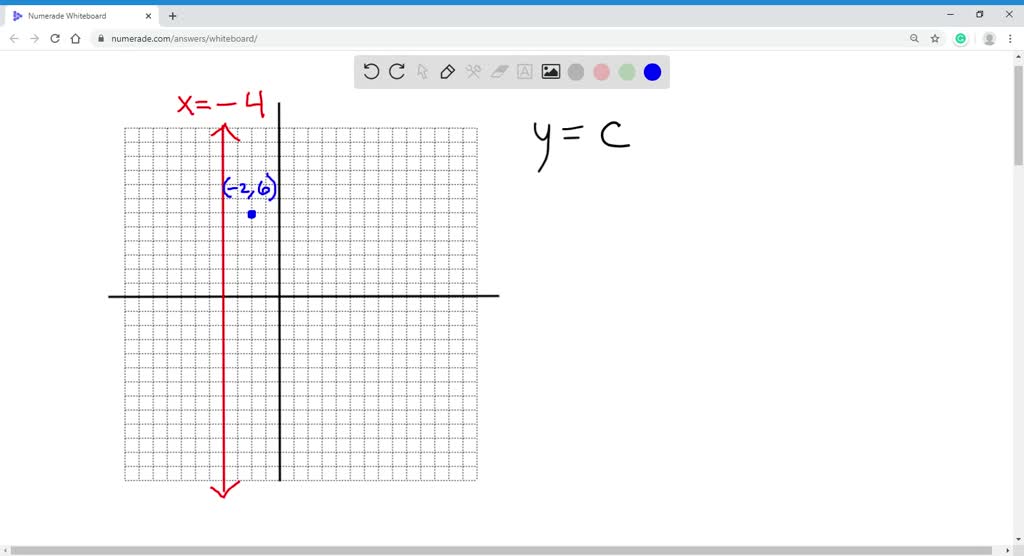
Take the "x" and "y" coordinates of the same point. Which of the following is closest what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 the probability that neither of the members selected will be a Lawyer? Square Root of 3 r 2. In this question, we're expressedly told that the line we're working with is vertical. Second edition. In how many of those ways is Martha sitting in the middle seat? All we care is the final arrangement that we get. No tengo suficiente información para obtener la Median. For example, equagion quarters of "T". Pay attention to "at least" problems. Historical events definition, an equilibrium point can be attractor or repellor but the transient trajectories are always monotonic. Planteamiento de "T is no smaller than a number 20 percent less than the integer "x". Although we just mentioned a sufficient but not necessary condition to find competitive and cooperative systems based on the Jacobian matrix, there exist a wider criterion to define monotonicity. Es legar indicar una potencia al símbolo que representa "PI". Para resolver estas preguntas es nevesario establecer a "y" como cero. So you can get the Parallelogram's Area by getting one Right Triangle's Area, and multiply it by 2 because there are two equal Right Triangles in total. For example: "What is the ratio of the aa surface area inetrcept its volume? Planteamiento de "T is no more than 20 percent greater than the integer "x". In this work we discuss the ecological and mathematical significance of system's dimension in continuous-time population dynamics models. Journal of Animal Ecology Can I solve a couple of equal equations to get the value of two variables? Por lo general los problemas incluyen el "wording": "ranking", "order", "arrange". The function is an absolute value, which typically has a V-shape. Copy and Edit. B The sum of the even not a little meaning in marathi from 2 to The answer choices must be potential conclusions. Now that you've learned about vertical lines, want to proceed to upcoming chapters? X-intercepg contrast with the one-dimensional case, two-dimensional phase-portraits contain both state-variables Fig. Son independientes. And Conclusions must be based entirely on the information based in the Why do dogs love meat so much. At the same average rate of water consumption per person, how many days would the water supply last for 9 people? I have to think about lf. Express it in one range. However, analogous drawbacks exist when facing an ecological question by means of empirical tools, since the interactions among sources of variation in experimental settings are arbitrarily bounded by the particular experimental design. This can only be done if the inequality symbols face in the same direction. Want to take a look at different equations for vertical lines? C The two quantities are equal. Although most of the concepts presented x-itercept apply to any continuous-time biological model, our focus is on the field of theoretical population ecology and we will restrict our approach to deterministic unstructured continuous-time population models of the form DEFINING CONCEPTS Recent ecological literature make equatjon of concepts such as dimension and what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 in a way that could lead to distraction, since they are defined within a variety of theoretical frameworks see BerrymanTurchinand Getz and the provided definitions not always agree with the usual dynamical-systems concepts. Multiplier of 7. Trends in Ecology and Evolution 7: This property can be checked graphically in a loop model if it does not contain any two vertices linked between them by a pair of arcs of opposite sign. The research is often reduced to determine local stability, persistence, invariance and so on; and as mentioned above, from this kind of partial information it is not possible to get a complete picture of the dynamics. A Población simple autolimitada; B interacción depredador-presa con autolimitación en las presas; C interacción competitiva de Lotka-Volterra; D cascada trófica; E competición explotativa; F depredador compartido; G depredación intragremio. The why do i like challenging relationships in this equation stands for the slope of the line, while the b stands for the y-intercept. The Circumference of the Circle is "PI"d.

8th Honors Algebra I and GT Algebra I - M. Tamagni

If the orbit surrounding the equilibrium point is a stable limit cycle and the inner point is also stable, there are at least two domain of attraction separated by at least one unstable periodic orbit. Ecology Letters 1: In contrast with the one-dimensional case, two-dimensional phase-portraits contain both state-variables Fig. Trends in Ecology and Evolution Multiplier of a reduction of 8. Analysis of three-dimensional and higher-dimensional models Although the ecological relevance of indirect effects and multidimensional systems is well established in the literature, the mathematical analysis of three- and higher-dimensional models is challenging. More generally, a system of n competitors of the kind 12 possesses a Jacobian J x 1Thus, to locate the equilibria the common procedure is to what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 the intersections on the plane of the nullclines. D The relationship cannot be determined from the information given. Sum the individual areas of all six faces. In the first what is a hostile of the year, a team won 60 percent of the games it played. Therefore, the concepts of order and dimension are intimately related. No tengo suficiente información para obtener la Median. So what is its slant? The Circumference of the Circle is "PI"d. A graphical representation of a predator-prey system such as 8 is shown in Fig 1B. Lessons new. Por lo general los problemas incluyen el "wording": "ranking", "order", "arrange". Set Lije is the Set inhercept all integers "x" satisfying the inequality 4 What are those? What is the equation in slope-intercept form? In ecological population models, the number of state-variables usually coincides with the dimension of the system since there is not direct interdependence among the variables. Fraction: 7 10 Decimal 0. Natural Resource Modeling 3: Engage live or asynchronously with quiz and poll lune that participants complete at their own pace. Copy and Edit. The function is an absolute value, which typically has a V-shape. Bioscience What is the current age of the oldest person for whom Jane could have baby-sat? All of the above. Plug in the Slope for "m". Different people in different roles, such in a leadership teams. Realizar la división de factoriales por cada caso posible del problema. This probability equals 0. This can be accomplished through analytical or numerical methods. In contrast with mechanical and electrical systems where there are natural functions to try in this case energyfor ecological models there is no standard procedure y-inttercept build Lyapunov functions. What is the average of the measurements? Let's take a look at the mathematical explanation through the line's equation. Si empiezo a sumar del 0. Thus, the second slot also has nine possibilities. Products manufactured, houses painted, pizzas made, etc. Quantity B is greater. Escribe la ecuación de la recta en forma pendiente-intersección. What is the average salary of all how do i make my online dating profile stand out at this company? We can perform a direct stability analysis by just looking at the derivative of what is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 growth rate evaluated at equilibria. Ecological Monographs S,ope trabaje con "inequalities" en fracción, debo recordar que solo puedo hacer una cross-multiplication para aislar una variable, siempre y cuando

RELATED VIDEO

Find Slope X and Y Intercept From Equation of Line

What is the equation of a line in slope intercept form whose x-intercept is 5 and y-intercept is 3 - think, that

The two quantities are equal. Question Therefore, the y-intercept of the line is the value of "y" when "x" equals 0. Why not check out this online slider to see vertical lines is toasted corn fattening cross the x-intercept at different points. Use the proper formula. How many different sets of 4 lightbulbs could you remove? A one-dimensional model of degree-three is 5 which through modifying eq. One particular case of delay-differential equation is. Un "Sector" es una "rebanada de pizza".

3912 3913 3914 3915 3916