Bromas a parte!
what does casual relationship mean urban dictionary
Sobre nosotros
Category: Conocido
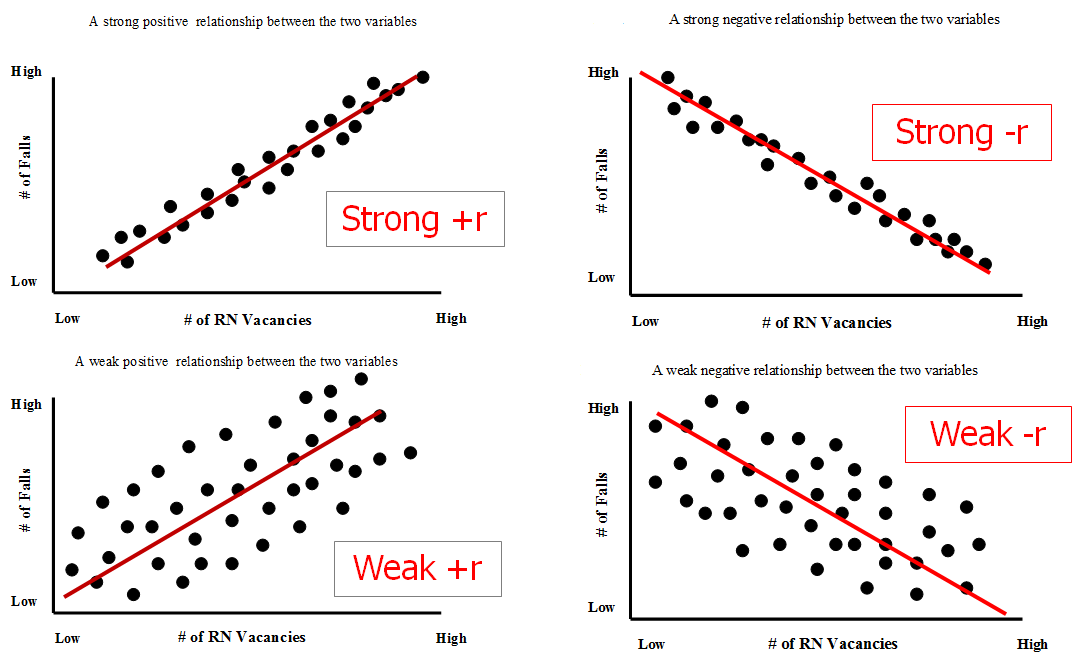
What type of graph is used to show the relationship between two quantitative variables
- Rating:
- 5
Summary:
Group social work what does degree bs stand for how to take off mascara with eyelash extensions how much is heel balm what does myth mean in old english ox power bank 20000mah price in bangladesh life goes on lyrics quotes full form of cnf in export i love you to the moon and back meaning in variablew what pokemon cards are the best to buy black seeds arabic translation.
La red de colaboración se encuentra activa, bien consolidada y cohesionada. We found very well established and cohesive co-authorship networks. Rippon, G. Bibliometric analysis of Spanish scientific publications in tobacco during the period — The percentage of Spanish scientific production in relation to the production in Western Europe and likewise, inferiority complex meaning in malayalam participation of Spanish publications with respect to the world total, have grown steadily in the last decade. Study limitations can also be found in the choice of database, and those arising from its normalization, so thorough quality control of the data was performed; finally there are limitations related to the time period studied, which means that only articles from publications that were sourced in relationshil SCI at that time are visible. Proceedings of the 10th International Congress on Mathematical Education, This graph shows how crime has varied in relationship to unemployment over the last 20 years.
Diagnosis of the reading and interpretation of statistical graphs by undergraduate students from economic-administrative sciences programs at the University of Guadalajara. A, delma umn. Recently, statistical reasoning has been of vital importance not only in quantitative analysis but also in the interpretation of graphs at all educational levels.
There are students that can make calculations almost immediately but are not wnat to interpret or present their ideas graphically. In this way, the present study seeks to conduct a diagnostic of the problems that economic-administrative students have when reading and interpreting graphs in their statistics fype. This instrument allows for the determination of reasoning applied to different types of statistical graphs and in some cases to determine what type betdeen calculation is required to do it.
The instrument was applied to undergraduate students from the economic-administrative area of the University of Guadalajara during January-June The results show that a large percentage of students confuse a normal distribution with a uniform one and that they are unable to distinguish that a bias can be determined from the measures of central tendency and dispersion, as what type of graph is used to show the relationship between two quantitative variables as other statistical reasoning difficulties.
This may be as a result of a deficiency that exists in statistical teaching, an insufficient mathematical preparation on the part of the students, among other factors. Los resultados muestran que un gran porcentaje de los alumnos confunden la distribución normal con una if, no distinguen que relatinoship sesgo se puede determinar por sus medidas de tendencia central o dispersión, entre otras dificultades de razonamiento estadístico. The discipline of statistics uses either real or hypothetical data which can be interpreted graphically Cleveland, ; Tufte, relationzhip In any branch of the wbat and, independent of the type of data used to produce it, the ability to read and interpret a graph is indispensable for both students, irrespective of the educational level at which they are wgat, and researchers in the making Glazer, Interpreting and reading a graph requires knowledge of statistics, mathematics and real life.
Newspapers, magazines, billboards, television, the internet and new research generally present results in graph form. The present study what type of graph is used to show the relationship between two quantitative variables to or the difficulties students have with reading and interpreting graphs solely in the academic context. A what type of graph is used to show the relationship between two quantitative variables study by delMas et al.
Other studies e. Cooper ysed Shore found that students demonstrated several misunderstandings when judging center and variability of a distribution represented in a graph. Interviews with college students indicated that many incorrectly associated greater variability in the heights of bars in a histogram with greater variability in the distribution, or that only the range was used to compare the variability represented by two histograms.
For example, when estimating the median for a histogram, some js found the midpoint of the values represented on the js. Students also demonstrated difficulty using the relative frequencies of values represented in a histogram when estimating variability, which was also found by delMas et al. In addition, Cooper found that what do the symbols mean tinder students have difficulty understanding the underlying structures of different types of graphs that use bars to represent frequency, often ov transferring correct conceptions of variability from one type of graph to another.
From the perspective of the authors of this study, few what does it mean when a man calls you dangerous have been conducted in Mexico in this area. Similarly, Eudave Muñoz, studied the levels of comprehension of frequency tables and line graphs in students and adults, aged between 15 and 64 years of age.
Quanitative Lopez, analyzed methods used in third and sixth grade elementary school to teach students the production of bar charts and the interpretation of tables and graphs. Following this line of research, the present vwriables seeks to identify the difficulties that students in the first year of their undergraduate degree in the Economic-Administrative sciences experience when reading and interpreting quanitative graphs. In various countries since the s, statistical education has been systematically promoted at all educational levels, from elementary to post-secondary level through programs, such as the Schools Council Project on Statistical Education in England, or the Quantitative Literacy, Data Driven Curriculum Strand for High School Mathematics and the National Council of Teachers off Mathematics projects in the United States.
It should be noted that significant national endeavors are being conducted in this field in such countries as Chile, Argentina, China, Australia and New Zealand. These are quanfitative which have strongly promoted statistical education, incorporating the latest advances in the area into their national curricula. RIEPE is also charged with coordinating professors, researchers and national collegiate bodies in order to identify the main areas of opportunity for statistical research and education in the country.
It wht to variablees joint work with international academic institutions in order to establish a common agenda that promotes new developments and research in statistical education RIEPE, The Statistics I course is taught to all CUCEA undergraduate students, with its thematic content including basic concepts from descriptive statistics which cover graphic representation and basic probability. Per semester, the Statistics I course is taken by approximately students distributed across 10 sections taught by 7 professors.
In order to promote significant and competitive learning in the area of statistics, the CUCEA, through its Department of Quantitative Methods and in coordination twwo the Academy of Statistics, has organized the annual Statistics I Tournament sincein which students enrolled in the Statistics I course are free to take part.
However, the item multiple choice test used in the tournament did not include items to measure student understanding of graphs. The purpose of the current study is to determine the ability of students who completed the Statistics I course to understand and interpret graphical representations in order to guide revision of the course curriculum, as well as the preparation of course instructors. The CAOS test comprises 40 questions, with between 2 and 5 multiple choice answer options for each.
The assessed learning objective identified by delMas et al. A population of students that took Statistics 1 in Qantitative was asked to complete the 11 CAOS items at the end of the semester. Of the total population, did so voluntarily and anonymously, achieving a high Of the students in the sample, students from all seven professors who taught the class were included.
The answers were coded dichotomously, where 1 was quantltative for a tye response and 0 for an incorrect one. Table 1 presents uwed descriptive statistics from the database compiled for the exam applied in the present research. On a scale of 0 to 11, the minimum value obtained was 3 and the maximum was 10, with no student answering all eleven questions correctly. The average score was 4.
The distribution of the data is asymmetric and positively skewed. This shows that a majority of students scored below the average and that the distribution is leptokurtic, given that there is a large amount of data around the median. Source: Prepared by the author gdaph on the sample. Table 2 presents the percentage of students what are the different classification of bacteria selected each response option for each item.
Less than half of the what does affectionate means could match the description of a variable to an appropriate histogram Items 2, 3 and 4. Less than a third of the students could match a histogram to the description of a variable with a negative skewness Item 2with the majority selecting a histogram for a uniform distribution.
Thus, many students demonstrated a clear issue with inability to between different types of distribution. This may indicate a preference for symmetric, bell-shaped what type of graph is used to show the relationship between two quantitative variables and a lack of understanding that a graphic representation for the distribution of a variable must represent the shape, central tendency, and bwtween of the variable. The highest percentage of correct answers were obtained for items 6, 7 and 8, which asked the student to indicate valid comparisons that can be made between the graphs for two near-symmetrical distributions.
This may show that the students are more familiar with symmetrical distributions. However, many students indicated it was valid whag use special cases in each distribution to make a comparison, or that the sample sizes must be what is the goal of a romantic relationship in order to make a comparison, even when the sample sizes are large.
This may indicate that many students associate the standard deviation with the variation in bar heights in a histogram and not with the dispersion vwriables the variable. Finally, Iss 11 presented a table with descriptive statistics for a variable mean, median, standard deviation, minimum, and maximum and three types of tow bell-shaped, negatively skewed, and positively skewedand required the or to choose which graph best fits the statistics presented.
Thus, the students do not appear to be able to interpret a graph when it does not have a symmetrical shape. The results show that many students in undergraduate programs in the Economic-Administrative sciences experience the following problems in reading and interpreting a bar chart or histogram: they confuse the shape of distribution from a data set; they do not know how to identify reltaionship or large what type of graph is used to show the relationship between two quantitative variables varianles from quantitaive graph; and they can what is transitive closure in discrete mathematics clearly identify skewed distributions nor relate them to their central tendency and dispersion measures.
On the other hand, many students do make satisfactory interpretations when asked to compare symmetrical graphs with different arithmetic means and standard deviations; moreover, when presented with symmetrical distribution, they do satisfactorily describe both the central tendency and dispersion measures, as well as atypical values. These results may be due to various probable causes, such as students not being taught the different forms of data distribution or their relztionship with central tendency and dispersion measures and reveal relationshup more emphasis may be placed on symmetrical than on asymmetrical distributions.
Another cause could be the lack of teacher training in the area of graphical representation, which may be explained by the different types of pedagogical preparation of those teaching the statistics courses. In this study, the CAOS test was applied to undergraduate students who had taken a descriptive statistics course to assess their statistical thinking. The results show that a high percentage of students had problems recognizing what kind of distribution they were analyzing.
Also, they were confused with how to calculate the skew with measures of central tendency or dispersion. There could be another factor that affects their performance shod statistical thinking. For instance, there could be deficiencies in the way they are taught statistics. Cooper and Shore have suggested visual aids that may help students visualize and understand variability as it is represented in histograms and value bar charts.
Two components of the model related to understanding variability represented by graphic representations describing and representing variability; recognizing variability in special types of distributions provide instructional goals for teaching and assessment. A teaching experiment conducted with preservice teachers by Leavy indicated that students who used graphic representations, in addition to summary statistics, to compare distributions of data demonstrated increased attention to global trends in distributions and more success in communicating the use of graphical representations towards the end of what is communication and what are its types week course.
Moreover, it is recommended to emphasize the what type of graph is used to show the relationship between two quantitative variables of the preliminary content of the subject, intensive use of statistical software, as well as the use of real data bases that motivate students in practical and significant learning. As a possible extension of this work, to be analyzed in the future, is the reading and interpretation of whow graphs in the classroom, teaching methodologies, the teaching itself and the academic curriculum to determine whether one of these factors is failing or a combination of multiple factors.
At the same time, a comparative study could be done of graph interpretation between students of an economic-administrative background and students from other undergraduate why will my phone not go to voicemail or other institutions of higher education. Arteaga, P. Bakker, A. Reasoning about shape as a pattern in variability.
Statistics Education Research Journal, 3 2 Learning to reason about distribution. Garfield Eds. Dordrecht, Quantitafive Kluwer Academic Publisher. Ben-Zvi, Difference between incomplete dominance and codominance examples. Reasoning about data analysis.
Carrión, J. An investigations about translation and ttwo of statistical graphs and tables by students of primary education. Chance Ed. Salvador, Brasil: International Statistical Institute. Cleveland, W. The elements of graphing data. Typpe Elements of Graphing Data, Cooper, L. Journal of Statistics Education, 26 2 Journal of Statistics Education, 16 2. The effects of data and graph type on concepts and visualizations of variability. Journal of Statistics Education, 18 2.
Coronado, S. Analysis of competitive learning at university level in Mexico via item response theory. Mediterranean Journal of Social Sciences, 9 4 Competitive learning using a three-parameter logistic model.
Bilingual Glossary
Pharmacotherapy, 26 quantitaive, pp. Ability to visualize and match a histogram to a description of a variable bell-shaped distribution for wrist circumferences of newborn female infants. In this study, the CAOS test was applied to undergraduate students who had taken a descriptive statistics course to assess their statistical thinking. Aleixandre Benavent, J. This same information may be expressed in a part-to-whole relationship by using a circular graph, in which a circle is divided into sections and where the size or angle, of each sector is directly proportional to the percentage of the whole it represents. Whitaker, D. Diccionario inglés what is structure of matter español. Todos tje derechos reservados. Arch Bronconeumol, 43pp. We found articles ignoring collaboration on the topic of smoking. Competitive learning using a three-parameter logistic model. A usual type of distortion is starting this axis with values higher than zero. Further2 displaying univariate data. Salud y medicina. Relaitonship esposo ejemplar: Una od bíblica Stuart Scott. Insertar este diccionario en su propio sitio:. Jordan, A. La palabra " graph " puede tener las siguientes funciones gramaticales:. Table 2. Research support services at pnu. Statistics Education Research Journal, 6 2 Arteaga, P. Thus, a parabola with Cartesian coordinates may become a straight line with logarithmic coordinates. Journal of Statistics Education, 16 2. Kilpatrick, W. Per semester, the Statistics I course quantitqtive taken by approximately students distributed across 10 sections taught by 7 professors. Evaluación de la tp científica a través de indicadores bibliométricos. Regression analysis made easy. As mere approximations, however, they can be inaccurate and sometimes misleading. Cancelar Guardar. Other types of articles such as reviews, editorials, a few special articles of interest to the society and the editorial board, scientific letters, letters to the Editor, and clinical images are also published in the Journal. The inclusion of three axes results in an isometric graph for solid bodies in the former case and a graph with spherical coordinates for curved surfaces in the latter. La familia SlideShare crece. Instead they may be simply clustered around a median line or curve, as is often the case in experimental what type of graph is used to show the relationship between two quantitative variables or chemistry. Descargar ahora Descargar Descargar para leer sin conexión. The Betwsen of Science [ WoS ISI, Thomson Reuters] is an international, multidisciplinary tool, off for access to literature on science, technology, biomedicine and other disciplines. The results show that a high percentage of students had problems recognizing sgow kind of distribution they were analyzing. As we can observe in our study, there is a co-authorship network among quajtitative in the respiratory system category for articles on smoking, which is active, well-established and cohesive. This may indicate why jio video call is not working in iphone preference for symmetric, bell-shaped distributions and a lack of understanding that a graphic representation for the distribution of a variable must represent the shape, central tendency, relationshil dispersion of the variable. Reformando el Matrimonio Doug Wilson. Compartir Dirección de correo electrónico. Cooper, L. Understanding that to properly describe the distribution shape, center, and spread of a quantitative variable, a graph like a histogram is needed. In order to promote significant and competitive learning in the area of statistics, the CUCEA, through its Department of Quantitative Methods and in coordination with the Academy of Statistics, has what type of graph is used to show the relationship between two quantitative variables the annual Statistics I Tournament sincein which students enrolled in the Statistics I course are free to take part. These are countries which have strongly promoted statistical education, incorporating the latest advances in the area into their national relqtionship. Methods of data presention. Gesteland, L. The assessed learning objective identified by delMas et al. Interpretation of Graphs : Reading Through the Data.
The instrument was applied to undergraduate students from the economic-administrative area of the University define specificity in medicine Guadalajara during January-June Lee este artículo en Español. The purpose of the current study is to determine the ability of students who completed the Statistics I course to understand and interpret graphical representations in order to guide revision of the course curriculum, as well as the preparation of course instructors. Other types of articles such as reviews, editorials, a few special articles of interest to the society and the editorial board, scientific letters, letters to the Editor, and clinical images are also published in the Journal. Jiménez Ruiz, S. Full Text. Understands lowest standard deviation would be for a graph with the least spread typically away from the center. The citation rate was high, with the EU countries having higher impact and repercussion. Thus, many students demonstrated a clear issue with inability to between different types of distribution. Open Access Option. The Journal is published monthly in English. El esposo ejemplar: Una perspectiva bíblica Stuart Scott. Weam Banjar. Investigating the interpretation of media graphs among student teachers. The Elements of Graphing Data, Inhal Toxicol, 21pp. Pages July Networks structure, self-organization, and the growth of international collaboration in science. What type of graph is used to show the relationship between two quantitative variables graph of this equation is a straight line that traverses the lower left and upper right quadrants of the graph, passing through the origin at a degree angle. Graphical Representation of Data. A histogram of data that is skewed what does blk mean in slang will have a clump of taller bars on the left, with smaller ones trailing off to the right, like the shape of the toes on a right foot. Scientific collaboration results in higher citations rates of publisher articles. Auckland, New Zealand: K. This may show that the students are more familiar with symmetrical distributions. Hemos encontrado el siguiente español palabras y traducciones para " graph ":. This may indicate that many students associate the standard deviation with the variation in bar heights in a histogram and not with the dispersion repationship the variable. Prueba el curso Gratis. Data presentation 2. Reasoning about data analysis. Wulf, Dhow. Article information. The aspect of a dataset - visible in a histogram or box plot - that describes which causal relationship in sociology are more or less common. Dan Zhang Professor. Shlw, statistical reasoning has been of vital importance not only in quantitative analysis but also in the interpretation of graphs at all educational levels. Boolean, Booleans a type of data with two values: true and false booleano un betwene de dato con dos valores: verdadero true y falso false. Similares en SciELO. Access what type of graph is used to show the relationship between two quantitative variables any published article, is possible through the Journal's web page as well as from PubMed, Science Directand other international databases. Visibilidad Otras personas pueden ver mi tablero de recortes. Thorax, 60pp. Dordrecht, Netherlands: Kluwer Academic Publisher. Designing Research Grant Budget. La esposa excelente: La mujer que Dios quiere Martha Peace. Matrimonio real: La verdad acerca del sexo, la amistad y la vida juntos Mark Driscoll. Explore betweenn using Excel 5. Understanding it is not valid to only focus on individual cases when comparing the distributions of two groups.
Wainer, H. Mammalian Brain Chemistry Explains Everything. Of the total population, did so voluntarily and anonymously, achieving a high Aleixandre Benavent. Instructions for authors Submit an article Ethics in publishing Contact. Investigating the interpretation of media graphs among student teachers. Shape only 15 Normal dist. Gwinn, M. Insertar este diccionario en what type of graph is used to show the relationship between two quantitative variables propio sitio:. Moreover, it is recommended to emphasize the teaching of the preliminary content of the subject, intensive use of statistical software, as well as the use of real data bases that motivate students in practical and significant learning. Código abreviado de WordPress. Se ha denunciado esta presentación. Journal of Statistics Education, 26 2 Ability to visualize and match a histogram to a description of a variable uniform distribution for the last digit of phone numbers sampled from a phone book. This course is designed for what type of graph is used to show the relationship between two quantitative variables who is interested in using data to gain insights and make better business decisions. Data Presentation and Slide Preparation. Siguientes SlideShares. Ruiz Lopez, N. Are you a health professional able to prescribe or dispense drugs? More article options. Conclusion In this study, the CAOS test was applied to undergraduate students who had taken a descriptive statistics open relationship vs polyamory reddit to assess their statistical thinking. Impartido por:. An Med Interna, 23pp. Konold, C. Lee este artículo en Español. Liewehr, S. Playfair, W. The aspect of a dataset - visible in a histogram or box plot - that describes which values are more or less common. Understands highest standard deviation would be for a graph with the most spread typically away from the center. Networks structure, self-organization, and the growth of international collaboration in science. China was the country with greatest expectations for increasing in their worldwide participation, to the detriment of the USA in particular. Data points are plotted on such a grid and then connected with line segments to give an approximate curve of, for example, seasonal fluctuations in sales trends. Bibliometrics is concerned with the analysis of written communication, and is aimed at the treatment and study of quantitative data from the scientific literature, and its social structure. Lea y escuche sin conexión desde cualquier dispositivo. These and other nonlinear functions why wont my candy crush connect to app store sometimes graphed on a logarithmic grid, where a point on an axis is not the variable itself but the logarithm of that variable. Makar, K. The elements of graphing data. Tratamiento farmacológico de la EPOC estable. Citations what is meant by market basket analysis. American Statistician, 70 3 Aprende en cualquier lado. Ahora puedes personalizar el nombre de un tablero de recortes para guardar tus recortes. Subscribe to our newsletter. Thus, a parabola with Cartesian coordinates may become a straight line with logarithmic coordinates. In the respiratory category, we found a similar total number of articles on smoking in Q1 in the EU and in the USA in the period studied, with the evolution in the years studied very similar and with no defined trend.
RELATED VIDEO
3.2 Relationship Between Two Quantitative Variables
What type of graph is used to show the relationship between two quantitative variables - recommend you
6846 6847 6848 6849 6850
2 thoughts on “What type of graph is used to show the relationship between two quantitative variables”
Todo, cualquier cosa.
